Math Initiative Bill Online
2010 Session
-Sponsor declined to post the bill due to economic circumstances. Good news: some schools are piloting the program anyway.
2009 Session
SB 159 Text
SB 159 Status
Singapore Bar Model Example - Brilliant
Singapore Math example set in Narnia
Full MA Study (Summary / Detail Report)
Longitudinal Study Released-Singapore Math WORKS-early release-Presentation by Dr. Bisk from Massachusetts
Presentation to Utah Legislature Education Committee on 9-17-08 (free download)
Dr. Yeap Ban Har's Singapore Math Powerpoint Presentation in Utah on 6-12-08 (free download)
Singapore Math: Simple or Complex (article)

Agency Based Education
Resources
This page is to provide some support documents for the letter of recommendations. It is not meant to be a comprehensive list, but an explanation of where the thought processes came from that went into the document. Some of the information presented here is duplicated from the Singapore Math Facts page.
Item 1: Curriculum
From E.D. Hirsch's Core Knowledge website:
"Math programs that follow sound cognitive principles and therefore lead to greater student mastery are: Singapore Math, Saxon Math, and Direct Instruction mathematics...
Singapore ranked first in the world in math and third in science, in spite of the fact that the country was ranked next to last for the level of home educational resources available. In other words, Singapore’s impressive academic results seem to have very little to do with an advantageous home environment and a great deal to do with an effective school system structure organized around a solid, rigorous curriculum."
John Hoven, PhD (Economist in the Antitrust Division of the U.S. Department of Justice; Co-president of the Gifted and Talented Association of Montgomery County, MD):
"NAEP classifies its problems as “easy,” “medium,” or “hard.” I benchmarked the “hard” 8th grade problems, examining NAEP’s highest level of expectation for 8th grade math. Most of these “hard” 8th grade problems are at the level of Singapore’s grade 5 – or lower."
Why Singapore Math?
Singapore math is a brilliantly laid out program that teaches students simple (and visual) tools to address complex problems. It is not spoon fed math, but asks students to think beyond simple single step problems all too common in American texts. In Singapore, students prove answers to understand why math works the way it does. It's an absolute science and Singapore gives students the opportunity to delve deeply into comprehending this beautiful language.
Here are some resources in the media and other articles which you can learn more about this program.
Comparing Singapore Math to Investigations Math
In L.A., Singapore Math has Added Value
Singapore Math: Simple or Complex?
Examples of Singapore Math Homework Pages
Here are some examples of Singapore math challenging word problems.
2nd grade: A toy bear weighs 12 oz. It is 7 oz lighter than a toy seal.
a) what is the weight of the toy seal?
b) how much do the two toys weigh altogether?
2nd grade: Alex had the same amount of money as Patrick. Alex saved another $72 and Patrick spent $19. How much more money did Alex have than Patrick in the end?
5th grade: Ryan has three times as many stamps as Hal and twice as many stamps as Jimmy. If they have 220 stamps altogether, how many more stamps does Jimmy have than Hal?
5th grade: Wendy and Tania had 130 rubber bands altogether. After Wendy gave away 1/5 of her rubber bands and Tania gave away 40 of her rubber bands, each girl had the same number of rubber bands left. How many rubber bands did Tania have at first?
Why not use Saxon math?
Saxon is a top notch program and in selecting Singapore math over it we do not say it is not a great program to use. Saxon is used by 8 out of the top 10 private schools in Utah as well as most charter schools and many public schools. It is a very effective program for teaching math, especially so if teachers are not very math fluent themselves which is especially the case in younger grades.
However, we want teachers that are math fluent. We want teachers who understand the math they are to teach. Singapore math demands that, and where teachers are trained the results are superior.
In Arizona, the top school for several years on state tests was a Saxon school. In a recent round of testing they were passed up by a school that implemented Singapore math. In other areas of the country, Singapore's success is being taken note of. In a recent article concerning Los Angeles schools that were using Singapore math, huge improvements in scores were pouring in after just a year on the program. (LA Times)
Singapore math is catching fire across the country and for good reason. It's been proven to work very well for the last 12 years as the world leader.
Why only use one program?
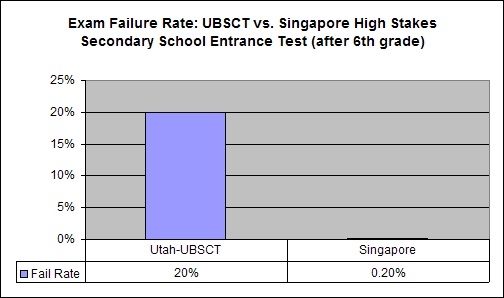
A common argument against standardizing on a math program is that no one program meets everyone's needs. This can be true if the program being used is deficient in one of the areas that students might need to learn from. However, Singapore math, requires virtually no remediation and every student learns. In block 3 below you will see a graph that shows Singapore's students have a 0.2% remediation rate for those that don't pass a high-stakes test after 6th grade. Furthermore, after one year in remediation, those students are ready to proceed. In Utah, 20% of our seniors can't pass the UBSCT. Singapore math is as close to a silver bullet as anything available. It is visual, auditory (mental math), tactile (manipulatives), and rigorous. With Singapore math there is no need for another program.
Item 2: Standards
Some of these support items are addressed on the home page but duplicated here to provide additional information.
Utah: Our state standards received a D from the Fordham Foundation and a C from the U.S. Chamber of Commerce.
Singapore: It is generally acknowledged that Singapore has some of the cleanest and smallest standards in the world. Where Utah may have 60 standards in a grade level, Singapore may have 15-20. Less topics equals greater time per topic, which means greater depth of knowledge.

In 2007, after enormous efforts to get our state math standards raised, a committee was chosen to do so but failed to follow the directions given to them. The legislature had instructed them to create standards that would result in "world class standards" but the people in charge of the committee merely sought a revision instead of a rewrite. They also neglected to compare our standards to top countries like Singapore and Japan. While the new standards are an improvement, they are not what they need to be for our children to get the education they need. For more on the history of the Utah standards issue and why they still need revised, see these pages:
http://www.oaknorton.com/mathupdates/20070811.cfm
http://www.oaknorton.com/mathupdates/20070926.cfm
To see the Singapore primary math standards:
http://www.moe.gov.sg/education/syllabuses/sciences/files/maths-primary-2001.pdf
http://www.moe.gov.sg/education/syllabuses/sciences/files/maths-primary-2007.pdf
Item 3: Assessments/Testing
Poll: Math, yes; standardized tests, maybe (AP/Yahoo News)
Will school testing overhaul make the grade? (Salt Lake Tribune)
Skill-test failures frustrate lawmakers (Deseret News)
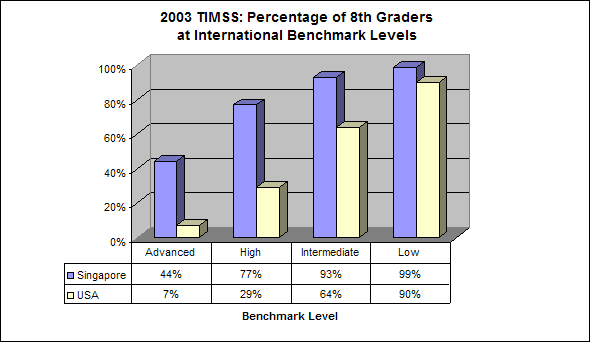
Compared to the United States as a whole on the last TIMSS exam, Singapore has 44% of their 8th graders at an advanced comprehension of math, while the United States languishes at 7%. WE CAN DO BETTER! Imagine a state where 40% of the population had an advanced understanding of math. Think of the high tech companies with high paying jobs that would flock to a state with that kind of workforce and vision. Utah can and should lead the country by adopting Singapore math.
Comparing our test failure rates, this chart shows Utah's UBSCT test administered to students graduating and shows that 20% of them can't pass 8th grade math work by the time they graduate. In Singapore, in order to move from elementary school to secondary school you must pass a high-stakes exam which has challenging questions on it. The difference is drastic.
Utah: Compared to peer states we rank dead last in math scores (Deseret News 11/2/07).
Singapore: Compared to the world, Singapore ranks #1 for 12 years running on TIMSS exams.
Item 4: Algebra
"Statistics from the U.S. Department of Education show that success in secondary school algebra is the single greatest predictor of success in college--not just for engineering and science majors, but for majors in all fields."
Los Angeles Times
Friday, September 17, 1999
It is important as we move forward that we have a cohesive system of education, especially in the K-8 range, which consistently and efficiently moves children into the all critical algebra program with a solid foundation. For that reason we are recommending that Singapore math be used K-8. Above that grade we can examine other strong programs for upper coursework.
From the Final Report of the National Mathematics Advisory Panel:
http://www.ed.gov/about/bdscomm/list/mathpanel/index.html
"All school districts should ensure that all prepared students have access to an authentic algebra course—and should prepare more students than at present to enroll in such a course by Grade 8. The word authentic is used here as a descriptor of a course that addresses algebra consistently with the Major Topics of School Algebra (Table 1, page 16). Students must be prepared with the mathematical prerequisites for this course according to the Critical Foundations of Algebra (page 17) and the Benchmarks for the Critical Foundations (Table 2, page 20)." (pg. 23)
Item 5: Student Progress
Students are different. There are some students who are more advanced than others, especially in a very specific subject area like math. Those students should have the opportunity to progress faster than other students to avoid the boredom that results from their mind not being stimulated at the pace they need. Conversely, students challenged by a subject should be able to receive remedial help. In Singapore, only a tiny fraction of their students (0.2%) have not mastered their basic skills by the end of 6th grade. Their curriculum places a premium on ensuring the basics are mastered sufficiently so that students can have success when they get to the critical algebra coursework.
From the Final Report of the National Mathematics Advisory Panel:
http://www.ed.gov/about/bdscomm/list/mathpanel/index.html
"Mathematically gifted students with sufficient motivation appear to be
able to learn mathematics much faster than students proceeding through
the curriculum at a normal pace, with no harm to their learning, and
should be allowed to do so." (pg. xxiv)
Item 6: Instruction time and schedule
Utah State Rule R277-419 requires local school boards to conduct school for at least 990 instructional hours and 180 days each school year. Most high schools in the state of Utah have switched from the seven period traditional schedule to the block schedule of eight periods with no increase in instruction time. Although the total instruction time is the same, the result of this switch is to take 1/8 of the instruction time out of each individual class to create the eighth class period. Thus important academic core courses such as English, math, science, and social sciences have lost 1/8 of the instruction time. One-eighth of 180 days is 22.5 school days or one whole month of instruction time.
Consider a chemistry class that meets on Tuesdays and Thursdays for a couple hours each time. If the student is sick on Thursday, he hasn't just missed one class, he's missed days of material that would have been taught Wednesday, Friday, and Monday, till the next class.
Difficult subjects require daily doses and pondering to integrate concepts into your mind. It's far easier to approach a topic in smaller chunks and retain knowledge than to take it in like a fire hose.
The National Council of Teachers of Mathematics recommends (http://www.nctm.org/about/content.aspx?id=6348), “All students need to be engaged in learning challenging mathematics for at least one hour a day at the elementary, middle school, and high school levels.”
Item 7: Mathematically knowledgeable classroom teachers
7a: Teacher preparation
Without strong math skills, teachers who teach math don't have the understanding of the subject necessary to pass those skills on to a student. Several studies have been done which bear this out and here are links to a couple of recent articles concerning it.
Study: USU Math Prep Faulty (Salt Lake Tribune)
Schools for teachers flunk math (AP/Provo Herald)
Five Standards for the Mathematics Preparation of Elementary Teachers
(http://www.nctq.org/p/publications/docs/nctq_ttmath_exec_summ.pdf)
Standard 1:
Aspiring elementary teachers must begin to acquire a deep conceptual knowledge of the mathematics that they will one day need to teach, moving well beyond mere procedural understanding. Required mathematics coursework should be tailored to the unique needs of the elementary teacher both in design and delivery, focusing on four critical areas:
1. numbers and operations,
2. algebra,
3. geometry and measurement, and — to a lesser degree —
4. data analysis and probability.
Standard 2:
Education schools should insist upon higher entry standards for admittance into their programs. As a condition for admission, aspiring elementary teachers should demonstrate that their knowledge of mathematics is at the high school level (geometry and coursework equivalent to second-year algebra). Appropriate tests include standardized achievement tests, college placement tests, and sufficiently rigorous high school exit tests.
Standard 3:
As conditions for completing their teacher preparation and earning a license, elementary teacher candidates should demonstrate a deeper understanding of mathematics content than is expected of children. Unfortunately, no current assessment is up to this task.
Standard 4:
Elementary content courses should be taught in close coordination with an elementary mathematics methods course that emphasizes numbers and operations. This course should provide numerous opportunities for students to practice-teach before elementary students, with emphasis placed on the delivery of mathematics content.
Standard 5:
The job of teaching aspiring elementary teachers mathematics content should be within the purview of mathematics departments. Careful attention must be paid to the selection of instructors with adequate professional qualifications in mathematics who appreciate the tremendous responsibility inherent in training the next generation of teachers and who understand the need to connect the mathematics topics to elementary classroom instruction.
NCTM President Skip Fennell:
"To boost teachers' understanding of math, the math departments at universities ought to place more emphasis on training educators, Fennell added."
"When I teach, at any level, the key question is always why?
I started using Singapore Math in professional development courses in 2000 as a vehicle to connect teacher knowledge of mathematical content with elementary and middle school student work. The biggest challenge we face in improving K-8 mathematics instruction is teacher content knowledge of the subject. We would never be satisfied if our third grade teachers read at the sixth grade level. But we have accepted that many operate mathematically at the sixth grade level. This is not meant to be a criticism of teachers; but rather of some of our teacher training programs and state departments that license teachers. Many elementary school teachers will readily admit that they don’t feel comfortable with mathematics. I believe that teacher content knowledge is critical and see the Singapore Math books as a vehicle for improving it. I also suspect that it’s the best elementary textbook series around."
7b: Teacher Leaders
Among schools and districts that implement Singapore math, it is common knowledge that the only way to do it right is to provide specific and direct training in the methodology Singapore uses. It is a bit different from a typical American classroom and focuses more heavily on the use of mental math. This focus allows students to build strong neural skills and increased concentration by breaking apart problems in their heads and being able to perform calculations much faster as they progress. Thus teachers must also be able to think through problems in this manner and be able to teach children to do so.
To learn this method cannot be done by book study but must be done by someone trained in the method. Utah will need a full time trainer in the state office that can put on workshops for district personnel either directly or via remote broadcast. This trainer must be someone highly skilled in this methodology that can create trainers in each district and support their efforts.
Not all teachers love math. Not all teachers can teach math. Those who can do it effectively and have a love for the subject are better prepared to transmit their knowledge to students and instill in the students a love for the subject. Those teachers should become specialists and focus on honing their skills to do that more effectively.
From the Final Report of the National Mathematics Advisory Panel:
"The Panel recommends that research be conducted on the use of full-time mathematics teachers in elementary schools. These would be teachers with strong knowledge of mathematics who would teach mathematics full-time to several classrooms of students, rather than teaching many subjects to one class, as is typical in most elementary classrooms. This recommendation for research is based on the Panel’s findings about the importance of teachers’ mathematical knowledge. The use of teachers who have specialized in elementary mathematics teaching could be a practical alternative to increasing all elementary teachers’ content knowledge (a problem of huge scale) by focusing the need for expertise on fewer teachers." (pg. xxii)
7c: Teacher Evaluation
In every profession there are professionals who are successful in their field and there are those who are not. Teachers are not exempt from this any more than accountants or engineers. Merit pay must be coupled with real accountability where teachers can be let go for not performing their jobs.
Districts statewide developing plans based on educator performance
From the Final Report of the National Mathematics Advisory Panel:
"Teachers who consistently produce significant gains in students’
mathematics achievement can be identified using value-added analyses
(analyses that examine individual students’ achievement gains as a
function of the teacher). The impact on students’ mathematics learning is compounded if students have a series of these more effective teachers." (pg. xx)
7d: Professional Development
Singapore teachers are entitled to 100 hours per year of professional development. Utah should adopt this practice (particularly for math) and gear the training in the content of the course materials.
Summer is the down-time of the year for teachers. They get time off and their pay reflects that they are not at work for a large portion of the year. Math teachers should have summer classes they attend that are approved by a mathematics department at a university to increase their knowledge of the subject matter. Science teachers should likewise have classes to attend. The teachers would be paid for their time taking the classes to further their professional development, and the classes would be paid for by the district.
From the Final Report of the National Mathematics Advisory Panel:
"The mathematics preparation of elementary and middle school teachers
must be strengthened as one means for improving teachers’ effectiveness in the classroom. This includes preservice teacher education, early career
support, and professional development programs. A critical component of
this recommendation is that teachers be given ample opportunities to learn mathematics for teaching. That is, teachers must know in detail and from a more advanced perspective the mathematical content they are responsible for teaching and the connections of that content to other important mathematics, both prior to and beyond the level they are assigned to teach." (pg. xxi)